Zbierka - Viacúčelová optimalizácia 3D modelov: Rozdiel medzi revíziami
(Vytvorená stránka „<div class="worksheet"> 360x360px|left|norotate=1 <h1>Voronoiove objekty - Blender</h1> <div class="section"> <div class="lesson-plan-text"> <div><div>Trvanie:</div><span>1.5 hod</span></div> <div><div>Náročnosť:</div><span>ťažký</span></div> <div><div>Zručnosti:</div><span>[https://kempelen.dai.fmph.uniba.sk/design/index.php/Cykly cykly], [https://kempelen.dai.fmph.uniba.sk/design/index.php/Podmienky…“) |
Bez shrnutí editace |
||
| (26 medziľahlých úprav od rovnakého používateľa nie je zobrazených.) | |||
| Riadok 1: | Riadok 1: | ||
<div class="worksheet"> | <div class="worksheet"> | ||
[[File:MOEA.stl|360x360px|left|norotate=1]] | [[File:MOEA.stl|360x360px|left|norotate=1]] | ||
<h1> | <h1>Viacúčelová optimalizácia 3D modelov</h1> | ||
<div class="section"> | <div class="section"> | ||
<div class="lesson-plan-text"> | <div class="lesson-plan-text"> | ||
<div><div>Trvanie:</div><span> | <div><div>Trvanie:</div><span>∞</span></div> | ||
<div><div>Náročnosť:</div><span>ťažký</span></div> | <div><div>Náročnosť:</div><span>ťažký</span></div> | ||
<div><div>Zručnosti:</div><span>[https://kempelen.dai.fmph.uniba.sk/design/index.php/Cykly cykly], [https://kempelen.dai.fmph.uniba.sk/design/index.php/Podmienky podmienky], [https://kempelen.dai.fmph.uniba.sk/design/index.php/Funkcie funkcie], [https://kempelen.dai.fmph.uniba.sk/design/index.php/Blender_Python_API práca s bpy]</span></div> | <div><div>Zručnosti:</div><span>[https://kempelen.dai.fmph.uniba.sk/design/index.php/Cykly cykly], [https://kempelen.dai.fmph.uniba.sk/design/index.php/Podmienky podmienky], [https://kempelen.dai.fmph.uniba.sk/design/index.php/Funkcie funkcie], [https://kempelen.dai.fmph.uniba.sk/design/index.php/Blender_Python_API práca s bpy] a [https://kempelen.dai.fmph.uniba.sk/design/index.php/Platypus s platypus]</span></div> | ||
<div><div>Nástroje:</div><span>[https://www.blender.org/ Blender], [https://www.python.org/ Python]</span></div> | |||
</div> | </div> | ||
<p>V predošlých úlohách sme sa naučili pracovať s prostredím Blender s použitím Pyhtonu. Teraz prechádzame do konceptu viacúčelovej optimalizácie, ktorú si vysvetlme a ukážeme. Definciou postačujúcou pre nás bude v tomto prípade, že viacúčelová optimalizácia je proces hľadania najlepších možných riešení pre viacero súčasne sledovaných cieľov alebo kritérií. Cieľom je nájsť také riešenia, ktoré predstavujú tzv. Pareto-optimálnu množinu, kde nie je možné zlepšiť jedno kritérium bez zhoršenia niektorého z ostatných kritérií. Ide o vyhľadávanie riešení pomocou kompormisu, ktoré vyvažujú protichodné požiadavky rôznych cieľov. Vo viacúčelovej optimalizácii nie je jedno jednoznačne najlepšie riešenie, ale skupina riešení, nazývaná Pareto-optimálna fronta, medzi ktorými musí rozhodovať užívateľ na základe preferencií alebo ďalších kritérií.</p> | <p>V predošlých úlohách sme sa naučili pracovať s prostredím Blender s použitím Pyhtonu. Teraz prechádzame do konceptu viacúčelovej optimalizácie, ktorú si vysvetlme a ukážeme. Definciou postačujúcou pre nás bude v tomto prípade, že viacúčelová optimalizácia je proces hľadania najlepších možných riešení pre viacero súčasne sledovaných cieľov alebo kritérií. Cieľom je nájsť také riešenia, ktoré predstavujú tzv. Pareto-optimálnu množinu, kde nie je možné zlepšiť jedno kritérium bez zhoršenia niektorého z ostatných kritérií. Ide o vyhľadávanie riešení pomocou kompormisu, ktoré vyvažujú protichodné požiadavky rôznych cieľov. Vo viacúčelovej optimalizácii nie je jedno jednoznačne najlepšie riešenie, ale skupina riešení, nazývaná Pareto-optimálna fronta, medzi ktorými musí rozhodovať užívateľ na základe preferencií alebo ďalších kritérií.</p> | ||
| Riadok 15: | Riadok 15: | ||
<div class="section"> | <div class="section"> | ||
<h3>Zadanie úlohy</h3> | <h3>Zadanie úlohy</h3> | ||
<p>Cieľom tejto úlohy je | <p>Cieľom tejto úlohy je oboznámiť sa s knižnicou platypus pre prácu s viacúčelovou optimalizáciou, zistiť ako funguje, čo všetko na to potrebujeme, ktoré aspekty pri ladení musíme zohľadňovať, ak uvažovať o tom ako by sa takáto optimalizácia dala zovšeobecňovať. Viacúčelová optimaliácia je jedným zo spôsobov akým môžeme implementovať parametrické a generatívne modelovanie 3D objektov. Taktiež si vo väčšom precvičíme prácu s Blenderom a Pythonom a načíme sa nové programátorksé praktiky. V našom prípade nám pôjde o to definovať takú optimalizáciu, ktorá by vyhovovala naším požiadavkám. V prípade optimalizácie 3D modelu pomocou ich modifikácie nám ide o hľadanie tých najoptimálnejších parametrov, ktoré nám umožnia objekt meniť tak aby spĺňal kritériá, ktoré naň kladieme.</p> | ||
</div> | </div> | ||
| Riadok 24: | Riadok 24: | ||
<li>[https://kempelen.dai.fmph.uniba.sk/design/index.php/Te%C3%B3ria Teória] - rozcestník stručnej teórie pre koncepty, ktoré potrebujeme</li> | <li>[https://kempelen.dai.fmph.uniba.sk/design/index.php/Te%C3%B3ria Teória] - rozcestník stručnej teórie pre koncepty, ktoré potrebujeme</li> | ||
<li>[https://docs.blender.org/ Rozcestník dokumentácií Blendera] - nájdete tu dokumentáciu pre vývojárov, používateľskú ríručku a aj Python API dokumentáciu</li> | <li>[https://docs.blender.org/ Rozcestník dokumentácií Blendera] - nájdete tu dokumentáciu pre vývojárov, používateľskú ríručku a aj Python API dokumentáciu</li> | ||
<li>[https://docs.python.org/3/tutorial/index.html Python syntax] - | <li>[https://docs.python.org/3/tutorial/index.html Python syntax] - syntax a použitie jazyka Python s ukážkami použitia</li> | ||
<li>[https://docs.blender.org/api/current/index.html Blender Python API] - dokumentácia Python API v Blenderi - nájdete tu všetko čo sa týka programovania s Python API (s knižnicou bpy) v Blenderi</li> | <li>[https://docs.blender.org/api/current/index.html Blender Python API] - dokumentácia Python API v Blenderi - nájdete tu všetko čo sa týka programovania s Python API (s knižnicou bpy) v Blenderi</li> | ||
<li>[https://platypus.readthedocs.io/en/stable/ Platypus] - dokumentácia knižnice Platypus s ukážkami použitia</li> | |||
</ul> | </ul> | ||
</div> | </div> | ||
| Riadok 32: | Riadok 33: | ||
<h3>Inštrukcie</h3> | <h3>Inštrukcie</h3> | ||
<ol> | <ol> | ||
<li>Zapneme si nástroj Blender a | <li>Zapneme si nástroj Blender a nastavíme si prostredie ako sme sa naučili v predošlých úlohách - necháme si v scéne objekt kocky, prepneme sa do režimu "Scripting" a vytvoríme si tam súbor, do ktorého budeme písať kód.</li> | ||
<li> | <li>Môžeme si skúsiť pripomenúť prácu s knižnicou bpy z minulých úloh pomocou volania niektorých funkcií. Pre túto úlohu ju budeme potrebovať.</li> | ||
<li> | <li>Ubezpečíme sa, že máme nainštalovanú knižnicu platypus - skúsime ju importovať pomocou<br> | ||
<pre> | |||
import platypus | |||
</pre> | |||
<li> | a skúsiť si zavolať nejaký príkaz. Ak nie je nainštalovaná, vieme si ju nainštalovať pomocou príkazu<br> | ||
<pre> | |||
import | import site | ||
import pip | |||
pip.main(['install', 'Platypus-Opt', '--target', site.USER_SITE]) | |||
</pre> | |||
</li> | |||
<li>Ďalej si vyskúšame prácu s knižnicou. Na tomto odkaze v teórii nájdeme príklad jej použitia: [https://platypus.readthedocs.io/en/stable/getting-started.html#a-simple-example príklad použitia platypus], príklad je stručne aj tu:<br> | |||
<pre> | |||
from platypus import NSGAII, Problem, Real | |||
def schaffer(x): | |||
return [x[0]**2, (x[0]-2)**2] | |||
problem = Problem(1, 2) | |||
problem.types[:] = Real(-10, 10) | |||
problem.function = schaffer | |||
[[File: | algorithm = NSGAII(problem) | ||
<li> | algorithm.run(10000) | ||
<li>Ďalej | </pre> | ||
Tento kód si vieme spustiť v Pythone a následne uvidíme výpis výsledkov optimalizácie problému. Ak ho nikde nevidíme, môžeme si otvoriť systémovú konzolu v Blenderi nasledovne:<br>[[File:Blender_system_console.png|312px]]<br>Toto je definícia problému s 1 premennou 2 cieľmi s funkciou schaffer(x), ktorá priradzuje týmto premenným hodnoty. Keby sme si zobrazili na grafe toto riešenie, vyzeralo by nasledovne:<br>[[File:schaffer_pareto.png|alt=obrázok grafu výsledku optimalizácie pomocou schaffer funkcie|320px]]<br> | |||
Na grafe vidíme Paretov front. Je to množina všetkých optimálnych riešení, ktorú budeme chcieť hľadať aj pri optimálizácii našich 3D modelov. Najprv však musíme definovať vlastný problém a vlastnú funkciu, ktorá bude slúžiť na ohodnotenie parametrov, ktoré sa budeme snažiť optimalizovať.</li> | |||
<li>Čo ak budeme chcieť optimalizovať viac ako 2 parametre? Aj toto knižnica Platypus dokáže, skúste si skopírovať qa spustiť nasledovný kód:<br> | |||
<pre> | |||
from platypus import NSGAII, Problem, Real | |||
import math | |||
def test_functions(x): | |||
return [math.sin(x[0]), math.cos(x[0]), x[0]**2] | |||
problem = Problem(1, 3) | |||
problem.types[:] = Real(-3, 3) | |||
problem.function = test_functions | |||
algorithm = NSGAII(problem) | |||
algorithm.run(10000) | |||
for s in algorithm.result: | |||
print("VARIABLES: ", s.variables) | |||
print("OBJECTIVES: ", s.objectives) | |||
# plot the results using matplotlib | |||
import matplotlib.pyplot as plt | |||
from mpl_toolkits.mplot3d import Axes3D | |||
fig = plt.figure() | |||
ax = fig.add_subplot(111, projection='3d') | |||
for s in algorithm.result: | |||
ax.scatter(s.objectives[0], s.objectives[1], s.objectives[2]) | |||
ax.set_xlabel('$f_1(x)=sin(x)$') | |||
ax.set_ylabel('$f_2(x)=cos(x)$') | |||
ax.set_zlabel('$f_3(x)=x^2$') | |||
plt.show() | |||
</pre> | |||
Ak ste všetko spravili správne, kód by vám mal vygenerovať takýto 3D graf:<br> | |||
[[File:pareto_front_3_params.png|alt=obrázok 3D grafu paretovho frontu|320px]] | |||
<br> | |||
Takže kým sa snažíme optimalizovať 2 alebo 3 parametre, vieme si to takto vizualizovať, no pri viacerých parametroch by výpovedná hodnota vizualizácie riešenia bola len veľmi nízka, takže my sa zameriame najmä na 2 či 3 parametre. | |||
</li> | |||
<li>Pre ďalšiu prácu si otvorte vzorové riešenie a môžete sledovať kód - v nasledovných inštrukciách si vysvetlíme fungovanie algoritmu.</li> | |||
<li>Optimalizovať budeme parametre meniace náš objekt. Týmito parametrami môže byť napríklad číslo škálovania objektu, alebo úroveň (levels) aplikácie levelu modifikátora "subdivision surface." Skúsme si preto vymyslieť modifikácie, ktoré budeme chcieť aplikovať a vytvorme si k ním funkcie podobné funkciám, ktoré inicializujú modifikácie z minulých cvičení. Takéto funkcie budeme potrebovať, pretože na to, aby sme dokázali ohodnotiť dané zmeny na objektu aby nám naša funkcia na hodnotenie vrátila validné hodnoty, musíme najskôr tieto zmeny na model aplikovať. Takouto funkciou je napríklad init_subdivision_modifier(obj, levels=1).</li> | |||
<li>Ďalej si definujeme problém. Potrebujeme si definovať počet parametrov a počet cieľov, ktoré chceme dosiahnuť. Náš problém bude definovaný ako Problem(3,3), pretože chceme definovať 3 ciele: veľkosť objektu, veľkosť počtu polygónov a hladkosť objektu, toto chceme to dosiahnuť úpravou 3 parametrov - škálovanie (scale), napríkald úroveň "decimate" modifikátora a úroveň levelu modifikátora "subdivision surface".</li> | |||
<li>Pre optimalizáciu slúži viac algoritmov, my si vyberieme NSGA-II. Môžete si naštudovať ostatné algoritmy v dokumentácii Platyus a posúdiť, na aké problémy by bol ktorý algoritmus vhodný. Niektoré totiž pracujú rýchlejšie, iné lepšie konvergujú ku konkrétnym hodnotám.</li> | |||
<li>Ďalej si potrebujeme vytvoriť našu hodnotiaciu funkciu (fitness funkciu) - niečo ako funkcia schaffer v počiatočnej ukážke. Táto funkcia slúži na pridelenie hodnotenia daným parametrom, ktoré náhodne algoritmus vygeneroval. Náhodne bude tieto hodnoty generovať z definície typov, ktoré mu určíme, napríklad takto:<br> | |||
<pre>problem.types[:] = [Real(0.5, 1), Real(0, 30), Real(0.5, 2)]</pre> | |||
Rovnako to vieme zapísať aj takto: | |||
<pre> | |||
problem.types[0] = Real(0.5, 1) | |||
problem.types[1] = Real(0, 30) | |||
problem.types[2] = Real(0.5, 2) | |||
</pre> | |||
kde prvý parameter určuje rozsahy ratio modifikátora "decimate",<br> | |||
druhý určuje levely modifikátora "subdivision surface"<br> | |||
tretí určuje škálovanie vo všetkých smeroch<br> | |||
a všetky sú typu Real, čo je nejaké desatinné číslo | |||
<br> | |||
Je potrebné dať si pozor aby typy boli rovnaké, inak by algoritmus nefungoval správne, je možné vytvoriť si Variator (nájdete v dokumentácii) alebo si môžete hodnoty nejakým spôsobom mapovať medzi sebou (čo robíme v prípade modifikátora "subdivision surface," ktorý dovoľuje len celé čísla v rozsahu 0 až 6), mapovanie nájdete v ukážkovom riešení. | |||
</li> | |||
<li>Potom je potrebné vytvoriť si fitness funkciu. Fitness funkcia (v našom prípade fitness_function) bude vždy brať parameter params, ktorý bude obsahovať n-ticu vygenerovaných náhodných parametrov na pozíciach v akom sme definovali typy daného problému. Tieto parametre budeme chcieť aplikovať na náš model a vyhodnotiť ho pomocou pomocných fitness funkcií, ako je v našom prípade napríklad get_surface_smoothness_fitness(object). Túto funkciu predávame algoritmu, aby ju spúšťal pri ohodnocovaní každého jedinca na náhodne generovaných parametroch, ktoré sme si definovali.<br> | |||
<pre> | |||
problem.function = fitness_function | |||
</pre> | |||
V našej implementácii si vytvoríme 3 fitness funkcie, kde jedna bude ohodnocovať hladkosť, druhá počet plôch objektu a tretia objem [https://en.wikipedia.org/wiki/Minimum_bounding_box bounding boxu]. Všetky sa budú volať v rámci hlavnej fitness_function: Najprv v nej robíme kopírovanie nášho objektu, aplikujeme naň modifikácie, vyhodnotíme ho pomocou našich pomocných fitness funkcií a nakoniec ho vymažeme aby nám nezostal zbytočne v scéne. Funkcia vracia n-ticu ohodnotení zodpovedajúcich parametrov na rovnakých indexoch. Je veľmi dôležité určiť si minimálne a maximálne hodnoty ak ich potrebujeme pre vytvorenie fitness funkcie. Fitness funkcie chceme mapovať na hodnoty 0 až 100, aby mali ohodnotenia daných parametrov rovnovážne obsadenie v optimalizácií. Musíme preto aj odhadnúť minimálne a maximálne hodnoty vo fitness funkciách podľa potreby. Napríklad vo funkcii get_faces_count_fitness(obj, min_faces, max_faces) musíme určiť minimálny a maximálny možný počet plôch, ktoré objekt môže obsahovať aby sme vedeli validne vyčísliť hodnotu. Ak napríklad pracujeme s objektom kocky, ktorá má v zkladnej verzii 6 plôch a modifikujeme ju do takej miery, že môže mať 100 plôch, môžeme si tieto okrajové hodnoty určiť napríklad od 4 do 200, no ak by sme mali komplexný objekt, takéto krajné hodnoty nemôžeme nechať takéto. Dajme tomu, že náš základný objekt má 100 plôch a chceme ho modifikovať pri čom sa môže znížiť aj zvýšiť počet plôch, podľa modifikácií, ktoré aplikujem - napríklad sudivision modifier vie exponenciálne zvýšiť počet plôch, v takom prípade by som si nastavil hodnotu max_faces napríklad na 100 000. Pri tvorbe fitness funkcií je potrebné zohľadniť tieto veci:<br> | |||
<ul> | |||
<li>možné rozsahy pred a po modifikácii objektu, čo sme si vysvetlili</li> | |||
<li>modifikácie, ktoré aplikujeme a zmeny, ktoré môžu v objektoch pred meraniami nastať - ak máme napríklad plochu tvorenú 3 bodmi, nemôžeme napríklad použiť modifikátor, ktorý znižuje počet bodov alebo hrán v objekte</li> | |||
<li>poradie aplikácie modifikátorov - iné poradie aplikovania modifikátorov môže kompletne zmeniť výsledný objekt</li> | |||
<li>rozumné rozsahy modifikácií - je potrebné zvážiť do akej miery chceme objekty modifikovať, pretože môže nastať, že objekt modifikujeme tak zložito, že výpočet môže trvať extrémne dlho, alebo môže celý program spadnúť</li> | |||
</ul> | |||
</li> | |||
<li>Celý proces optimalizácie sustíme nasledovne:<br> | |||
<pre> | |||
algorithm = NSGAII(problem, population_size=100) # optimalizačný algoritmus, ktorému predávame problém a veľkosť populácie | |||
algorithm.run(100) # hovoríme mu aby vytvoril 100 generácií a na nich optimalizoval dané vstupy | |||
</pre></li> | |||
<li>Výsledok optimalizácie získame z algorithm.result po dobehnutí optimalizácie, tento výsleodk obsahuje 2 polia, 1. sú generované premenné pri ktorých na zodpovedajúcom indexe ískali ohodnotenie v 2. poli. Takže prvé obsahuje premenné a druhé ich ohodnotenia. Z hodnôt objectives sa vytvára Paretov front. | |||
<pre> | |||
for solution in algorithm.result: | |||
print("Parameters:", solution.variables) | |||
print("Objectives:", solution.objectives) | |||
</pre> | |||
</li> | |||
<li>Ostáva nám tieto parametre si prejsť a aplikovať na náš model, toto robíme vo funkcii apply_parameters_and_position_objects(best_parameters, worst_parameters, o).</li> | |||
<li>Skúste si na základe poskytnutého kódu vytvoriť inú optimalizáciu, pozmeniť modifkátori alebo implementovať iné modifikácie objektov, iné hodnotiace funkcie. Vzorové riešenie obsahuje modifikácie, hodnotiace funkcie, inicializáciu problému a spustenie algoritmu, taktiež vykreslovanie ohodnotení / Paretovho frontu na grafe, výpis riešenia a vytvorenie niekoľkých modelov pomocou vygenerovaných parametrov a vytvorenie ich inštancií v scéne Blendera.</li> | |||
</ol> | </ol> | ||
</div> | </div> | ||
| Riadok 59: | Riadok 154: | ||
<div class="section"> | <div class="section"> | ||
<h3>Testovanie a úpravy</h3> | <h3>Testovanie a úpravy</h3> | ||
<p> | <p>Analyzujte či výsledky, ktoré váš optimalizačný algoritmus vracia sú relevantné a vieme ich zužitkovať, návrhy na vylepšenie máme tu:</p> | ||
<ul> | <ul> | ||
<li> | <li>skúste si odfiltrovať tie najlepšie a najhoršie ohodnotené riešenia optimalizačného algoritmu a vytvorit si podľa nich modely</li> | ||
<li> | <li>pokúste sa navrhnúť optimalizáciu ďalšieho parametra, to zahŕňa: vytvorenie fitness funkcie, špecifikácia typu a rozsahu parametru (prípadne jeho mapovanie), vytvorenie funkcie, ktorá dané modifikácie na model aplikuje</li> | ||
<li> | <li>vyskúšajte si importovať vlastný objekt a otestovať váš algoritmus na ňom</li> | ||
<li>vyskúšajte | <li>skúste implmentovať optimalizáciu pre rôzny počet parametrov a cieľov a sledujte ako to zmení výsledky</li> | ||
<li>namiesto algoritmu NSGA-II si vyskúšajte iné algoritmy ako napríklad NSGA-III, MOEAD a pozorujte rýchlosti výpočtu odchylky vo výsledkoch</li> | |||
</ul> | </ul> | ||
</div> | </div> | ||
| Riadok 79: | Riadok 168: | ||
<p>Ak budete potrebovať motiváciu alebo si skontrolovať váš výsledný model, v nasledujúcich odkazoch nájdete implementáciu daného modelu v nástrojoch, ktoré ste na implementáciu mohli použiť:</p> | <p>Ak budete potrebovať motiváciu alebo si skontrolovať váš výsledný model, v nasledujúcich odkazoch nájdete implementáciu daného modelu v nástrojoch, ktoré ste na implementáciu mohli použiť:</p> | ||
<ul> | <ul> | ||
<li>[https://github.com/Achinys-out/ParametricAndGenerativeDesign/blob/main/Python/ | <li>[https://github.com/Achinys-out/ParametricAndGenerativeDesign/blob/main/Python/multiobjective_3D_model_optimization.py Python]</li> | ||
</ul> | </ul> | ||
</div> | </div> | ||
| Riadok 85: | Riadok 174: | ||
<div class="section"> | <div class="section"> | ||
<h3>Záver</h3> | <h3>Záver</h3> | ||
<p>Týmto cvičením sme si | <p>Týmto cvičením sme si ukázali ako si dokážeme navrhnúť a vytvoriť vlastnú viacúčelovú optimalizáciu a vedieť s ňou vyriešiť vlastný problém, ktorý môže mať aj protichodné kritéria. Vieme na to využiť existujúce knižnice a aplikovať riešenie na výsledné modely. | ||
<br> | |||
Pre rozbehanie a prácu Blendera z Visual Studio Code potupujte podľa inštrukcii v tomto videu: [https://youtu.be/YUytEtaVrrc?si=Z5JsFinFzzHp3_Om Blender + VS Code].</p> | |||
</div> | </div> | ||
</div> | </div> | ||
Aktuálna revízia z 13:23, 10. máj 2024
Viacúčelová optimalizácia 3D modelov
V predošlých úlohách sme sa naučili pracovať s prostredím Blender s použitím Pyhtonu. Teraz prechádzame do konceptu viacúčelovej optimalizácie, ktorú si vysvetlme a ukážeme. Definciou postačujúcou pre nás bude v tomto prípade, že viacúčelová optimalizácia je proces hľadania najlepších možných riešení pre viacero súčasne sledovaných cieľov alebo kritérií. Cieľom je nájsť také riešenia, ktoré predstavujú tzv. Pareto-optimálnu množinu, kde nie je možné zlepšiť jedno kritérium bez zhoršenia niektorého z ostatných kritérií. Ide o vyhľadávanie riešení pomocou kompormisu, ktoré vyvažujú protichodné požiadavky rôznych cieľov. Vo viacúčelovej optimalizácii nie je jedno jednoznačne najlepšie riešenie, ale skupina riešení, nazývaná Pareto-optimálna fronta, medzi ktorými musí rozhodovať užívateľ na základe preferencií alebo ďalších kritérií.
Zadanie úlohy
Cieľom tejto úlohy je oboznámiť sa s knižnicou platypus pre prácu s viacúčelovou optimalizáciou, zistiť ako funguje, čo všetko na to potrebujeme, ktoré aspekty pri ladení musíme zohľadňovať, ak uvažovať o tom ako by sa takáto optimalizácia dala zovšeobecňovať. Viacúčelová optimaliácia je jedným zo spôsobov akým môžeme implementovať parametrické a generatívne modelovanie 3D objektov. Taktiež si vo väčšom precvičíme prácu s Blenderom a Pythonom a načíme sa nové programátorksé praktiky. V našom prípade nám pôjde o to definovať takú optimalizáciu, ktorá by vyhovovala naším požiadavkám. V prípade optimalizácie 3D modelu pomocou ich modifikácie nám ide o hľadanie tých najoptimálnejších parametrov, ktoré nám umožnia objekt meniť tak aby spĺňal kritériá, ktoré naň kladieme.
Odkazy na materiály
V tejto sekcii nájdete odkazy na materiály, ktoré vám môžu pomôcť pri riešení daných problémov a naučia vás ako používať požívané nástroje:
- Teória - rozcestník stručnej teórie pre koncepty, ktoré potrebujeme
- Rozcestník dokumentácií Blendera - nájdete tu dokumentáciu pre vývojárov, používateľskú ríručku a aj Python API dokumentáciu
- Python syntax - syntax a použitie jazyka Python s ukážkami použitia
- Blender Python API - dokumentácia Python API v Blenderi - nájdete tu všetko čo sa týka programovania s Python API (s knižnicou bpy) v Blenderi
- Platypus - dokumentácia knižnice Platypus s ukážkami použitia
Inštrukcie
- Zapneme si nástroj Blender a nastavíme si prostredie ako sme sa naučili v predošlých úlohách - necháme si v scéne objekt kocky, prepneme sa do režimu "Scripting" a vytvoríme si tam súbor, do ktorého budeme písať kód.
- Môžeme si skúsiť pripomenúť prácu s knižnicou bpy z minulých úloh pomocou volania niektorých funkcií. Pre túto úlohu ju budeme potrebovať.
- Ubezpečíme sa, že máme nainštalovanú knižnicu platypus - skúsime ju importovať pomocou
import platypus
a skúsiť si zavolať nejaký príkaz. Ak nie je nainštalovaná, vieme si ju nainštalovať pomocou príkazu
import site import pip pip.main(['install', 'Platypus-Opt', '--target', site.USER_SITE])
- Ďalej si vyskúšame prácu s knižnicou. Na tomto odkaze v teórii nájdeme príklad jej použitia: príklad použitia platypus, príklad je stručne aj tu:
from platypus import NSGAII, Problem, Real def schaffer(x): return [x[0]**2, (x[0]-2)**2] problem = Problem(1, 2) problem.types[:] = Real(-10, 10) problem.function = schaffer algorithm = NSGAII(problem) algorithm.run(10000)Tento kód si vieme spustiť v Pythone a následne uvidíme výpis výsledkov optimalizácie problému. Ak ho nikde nevidíme, môžeme si otvoriť systémovú konzolu v Blenderi nasledovne:
Na grafe vidíme Paretov front. Je to množina všetkých optimálnych riešení, ktorú budeme chcieť hľadať aj pri optimálizácii našich 3D modelov. Najprv však musíme definovať vlastný problém a vlastnú funkciu, ktorá bude slúžiť na ohodnotenie parametrov, ktoré sa budeme snažiť optimalizovať.
Toto je definícia problému s 1 premennou 2 cieľmi s funkciou schaffer(x), ktorá priradzuje týmto premenným hodnoty. Keby sme si zobrazili na grafe toto riešenie, vyzeralo by nasledovne: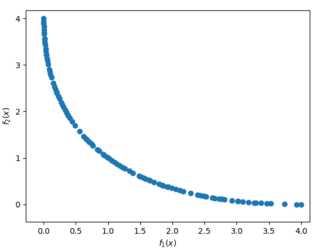
- Čo ak budeme chcieť optimalizovať viac ako 2 parametre? Aj toto knižnica Platypus dokáže, skúste si skopírovať qa spustiť nasledovný kód:
from platypus import NSGAII, Problem, Real import math def test_functions(x): return [math.sin(x[0]), math.cos(x[0]), x[0]**2] problem = Problem(1, 3) problem.types[:] = Real(-3, 3) problem.function = test_functions algorithm = NSGAII(problem) algorithm.run(10000) for s in algorithm.result: print("VARIABLES: ", s.variables) print("OBJECTIVES: ", s.objectives) # plot the results using matplotlib import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D fig = plt.figure() ax = fig.add_subplot(111, projection='3d') for s in algorithm.result: ax.scatter(s.objectives[0], s.objectives[1], s.objectives[2]) ax.set_xlabel('$f_1(x)=sin(x)$') ax.set_ylabel('$f_2(x)=cos(x)$') ax.set_zlabel('$f_3(x)=x^2$') plt.show()Ak ste všetko spravili správne, kód by vám mal vygenerovať takýto 3D graf:
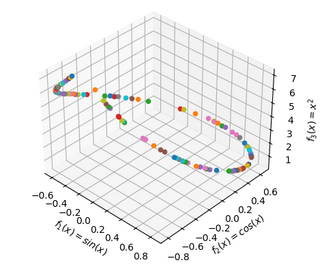
Takže kým sa snažíme optimalizovať 2 alebo 3 parametre, vieme si to takto vizualizovať, no pri viacerých parametroch by výpovedná hodnota vizualizácie riešenia bola len veľmi nízka, takže my sa zameriame najmä na 2 či 3 parametre. - Pre ďalšiu prácu si otvorte vzorové riešenie a môžete sledovať kód - v nasledovných inštrukciách si vysvetlíme fungovanie algoritmu.
- Optimalizovať budeme parametre meniace náš objekt. Týmito parametrami môže byť napríklad číslo škálovania objektu, alebo úroveň (levels) aplikácie levelu modifikátora "subdivision surface." Skúsme si preto vymyslieť modifikácie, ktoré budeme chcieť aplikovať a vytvorme si k ním funkcie podobné funkciám, ktoré inicializujú modifikácie z minulých cvičení. Takéto funkcie budeme potrebovať, pretože na to, aby sme dokázali ohodnotiť dané zmeny na objektu aby nám naša funkcia na hodnotenie vrátila validné hodnoty, musíme najskôr tieto zmeny na model aplikovať. Takouto funkciou je napríklad init_subdivision_modifier(obj, levels=1).
- Ďalej si definujeme problém. Potrebujeme si definovať počet parametrov a počet cieľov, ktoré chceme dosiahnuť. Náš problém bude definovaný ako Problem(3,3), pretože chceme definovať 3 ciele: veľkosť objektu, veľkosť počtu polygónov a hladkosť objektu, toto chceme to dosiahnuť úpravou 3 parametrov - škálovanie (scale), napríkald úroveň "decimate" modifikátora a úroveň levelu modifikátora "subdivision surface".
- Pre optimalizáciu slúži viac algoritmov, my si vyberieme NSGA-II. Môžete si naštudovať ostatné algoritmy v dokumentácii Platyus a posúdiť, na aké problémy by bol ktorý algoritmus vhodný. Niektoré totiž pracujú rýchlejšie, iné lepšie konvergujú ku konkrétnym hodnotám.
- Ďalej si potrebujeme vytvoriť našu hodnotiaciu funkciu (fitness funkciu) - niečo ako funkcia schaffer v počiatočnej ukážke. Táto funkcia slúži na pridelenie hodnotenia daným parametrom, ktoré náhodne algoritmus vygeneroval. Náhodne bude tieto hodnoty generovať z definície typov, ktoré mu určíme, napríklad takto:
problem.types[:] = [Real(0.5, 1), Real(0, 30), Real(0.5, 2)]
Rovnako to vieme zapísať aj takto:
problem.types[0] = Real(0.5, 1) problem.types[1] = Real(0, 30) problem.types[2] = Real(0.5, 2)
kde prvý parameter určuje rozsahy ratio modifikátora "decimate",
druhý určuje levely modifikátora "subdivision surface"
tretí určuje škálovanie vo všetkých smeroch
a všetky sú typu Real, čo je nejaké desatinné číslo
Je potrebné dať si pozor aby typy boli rovnaké, inak by algoritmus nefungoval správne, je možné vytvoriť si Variator (nájdete v dokumentácii) alebo si môžete hodnoty nejakým spôsobom mapovať medzi sebou (čo robíme v prípade modifikátora "subdivision surface," ktorý dovoľuje len celé čísla v rozsahu 0 až 6), mapovanie nájdete v ukážkovom riešení. - Potom je potrebné vytvoriť si fitness funkciu. Fitness funkcia (v našom prípade fitness_function) bude vždy brať parameter params, ktorý bude obsahovať n-ticu vygenerovaných náhodných parametrov na pozíciach v akom sme definovali typy daného problému. Tieto parametre budeme chcieť aplikovať na náš model a vyhodnotiť ho pomocou pomocných fitness funkcií, ako je v našom prípade napríklad get_surface_smoothness_fitness(object). Túto funkciu predávame algoritmu, aby ju spúšťal pri ohodnocovaní každého jedinca na náhodne generovaných parametroch, ktoré sme si definovali.
problem.function = fitness_function
V našej implementácii si vytvoríme 3 fitness funkcie, kde jedna bude ohodnocovať hladkosť, druhá počet plôch objektu a tretia objem bounding boxu. Všetky sa budú volať v rámci hlavnej fitness_function: Najprv v nej robíme kopírovanie nášho objektu, aplikujeme naň modifikácie, vyhodnotíme ho pomocou našich pomocných fitness funkcií a nakoniec ho vymažeme aby nám nezostal zbytočne v scéne. Funkcia vracia n-ticu ohodnotení zodpovedajúcich parametrov na rovnakých indexoch. Je veľmi dôležité určiť si minimálne a maximálne hodnoty ak ich potrebujeme pre vytvorenie fitness funkcie. Fitness funkcie chceme mapovať na hodnoty 0 až 100, aby mali ohodnotenia daných parametrov rovnovážne obsadenie v optimalizácií. Musíme preto aj odhadnúť minimálne a maximálne hodnoty vo fitness funkciách podľa potreby. Napríklad vo funkcii get_faces_count_fitness(obj, min_faces, max_faces) musíme určiť minimálny a maximálny možný počet plôch, ktoré objekt môže obsahovať aby sme vedeli validne vyčísliť hodnotu. Ak napríklad pracujeme s objektom kocky, ktorá má v zkladnej verzii 6 plôch a modifikujeme ju do takej miery, že môže mať 100 plôch, môžeme si tieto okrajové hodnoty určiť napríklad od 4 do 200, no ak by sme mali komplexný objekt, takéto krajné hodnoty nemôžeme nechať takéto. Dajme tomu, že náš základný objekt má 100 plôch a chceme ho modifikovať pri čom sa môže znížiť aj zvýšiť počet plôch, podľa modifikácií, ktoré aplikujem - napríklad sudivision modifier vie exponenciálne zvýšiť počet plôch, v takom prípade by som si nastavil hodnotu max_faces napríklad na 100 000. Pri tvorbe fitness funkcií je potrebné zohľadniť tieto veci:
- možné rozsahy pred a po modifikácii objektu, čo sme si vysvetlili
- modifikácie, ktoré aplikujeme a zmeny, ktoré môžu v objektoch pred meraniami nastať - ak máme napríklad plochu tvorenú 3 bodmi, nemôžeme napríklad použiť modifikátor, ktorý znižuje počet bodov alebo hrán v objekte
- poradie aplikácie modifikátorov - iné poradie aplikovania modifikátorov môže kompletne zmeniť výsledný objekt
- rozumné rozsahy modifikácií - je potrebné zvážiť do akej miery chceme objekty modifikovať, pretože môže nastať, že objekt modifikujeme tak zložito, že výpočet môže trvať extrémne dlho, alebo môže celý program spadnúť
- Celý proces optimalizácie sustíme nasledovne:
algorithm = NSGAII(problem, population_size=100) # optimalizačný algoritmus, ktorému predávame problém a veľkosť populácie algorithm.run(100) # hovoríme mu aby vytvoril 100 generácií a na nich optimalizoval dané vstupy
- Výsledok optimalizácie získame z algorithm.result po dobehnutí optimalizácie, tento výsleodk obsahuje 2 polia, 1. sú generované premenné pri ktorých na zodpovedajúcom indexe ískali ohodnotenie v 2. poli. Takže prvé obsahuje premenné a druhé ich ohodnotenia. Z hodnôt objectives sa vytvára Paretov front.
for solution in algorithm.result: print("Parameters:", solution.variables) print("Objectives:", solution.objectives) - Ostáva nám tieto parametre si prejsť a aplikovať na náš model, toto robíme vo funkcii apply_parameters_and_position_objects(best_parameters, worst_parameters, o).
- Skúste si na základe poskytnutého kódu vytvoriť inú optimalizáciu, pozmeniť modifkátori alebo implementovať iné modifikácie objektov, iné hodnotiace funkcie. Vzorové riešenie obsahuje modifikácie, hodnotiace funkcie, inicializáciu problému a spustenie algoritmu, taktiež vykreslovanie ohodnotení / Paretovho frontu na grafe, výpis riešenia a vytvorenie niekoľkých modelov pomocou vygenerovaných parametrov a vytvorenie ich inštancií v scéne Blendera.
Testovanie a úpravy
Analyzujte či výsledky, ktoré váš optimalizačný algoritmus vracia sú relevantné a vieme ich zužitkovať, návrhy na vylepšenie máme tu:
- skúste si odfiltrovať tie najlepšie a najhoršie ohodnotené riešenia optimalizačného algoritmu a vytvorit si podľa nich modely
- pokúste sa navrhnúť optimalizáciu ďalšieho parametra, to zahŕňa: vytvorenie fitness funkcie, špecifikácia typu a rozsahu parametru (prípadne jeho mapovanie), vytvorenie funkcie, ktorá dané modifikácie na model aplikuje
- vyskúšajte si importovať vlastný objekt a otestovať váš algoritmus na ňom
- skúste implmentovať optimalizáciu pre rôzny počet parametrov a cieľov a sledujte ako to zmení výsledky
- namiesto algoritmu NSGA-II si vyskúšajte iné algoritmy ako napríklad NSGA-III, MOEAD a pozorujte rýchlosti výpočtu odchylky vo výsledkoch
Vzorové riešenie
Ak budete potrebovať motiváciu alebo si skontrolovať váš výsledný model, v nasledujúcich odkazoch nájdete implementáciu daného modelu v nástrojoch, ktoré ste na implementáciu mohli použiť:
Záver
Týmto cvičením sme si ukázali ako si dokážeme navrhnúť a vytvoriť vlastnú viacúčelovú optimalizáciu a vedieť s ňou vyriešiť vlastný problém, ktorý môže mať aj protichodné kritéria. Vieme na to využiť existujúce knižnice a aplikovať riešenie na výsledné modely.
Pre rozbehanie a prácu Blendera z Visual Studio Code potupujte podľa inštrukcii v tomto videu: Blender + VS Code.
