Zbierka - Viacúčelová optimalizácia 3D modelov

   https://kempelen.dai.fmph.uniba.sk/design/images/4/4f/MOEA.stl

Viacúčelová optimalizácia 3D modelov

Trvanie:

2 hod

Náročnosť:

ťažký

Zručnosti:

cykly, podmienky, funkcie, práca s bpy a práca s platypus

Nástroje:

Blender

V predošlých úlohách sme sa naučili pracovať s prostredím Blender s použitím Pyhtonu. Teraz prechádzame do konceptu viacúčelovej optimalizácie, ktorú si vysvetlme a ukážeme. Definciou postačujúcou pre nás bude v tomto prípade, že viacúčelová optimalizácia je proces hľadania najlepších možných riešení pre viacero súčasne sledovaných cieľov alebo kritérií. Cieľom je nájsť také riešenia, ktoré predstavujú tzv. Pareto-optimálnu množinu, kde nie je možné zlepšiť jedno kritérium bez zhoršenia niektorého z ostatných kritérií. Ide o vyhľadávanie riešení pomocou kompormisu, ktoré vyvažujú protichodné požiadavky rôznych cieľov. Vo viacúčelovej optimalizácii nie je jedno jednoznačne najlepšie riešenie, ale skupina riešení, nazývaná Pareto-optimálna fronta, medzi ktorými musí rozhodovať užívateľ na základe preferencií alebo ďalších kritérií.

Zadanie úlohy

Cieľom tejto úlohy je oboznámiť sa s knižnicou platypus pre prácu s viacúčelovou optimalizáciou, zistiť ako funguje, čo všetko na to potrebujeme, ktoré aspekty pri ladení musíme zohľadňovať, ak uvažovať o tom ako by sa takáto optimalizácia dala zovšeobecňovať. Viacúčelová optimaliácia je jedným zo spôsobov akým môžeme implementovať parametrické a generatívne modelovanie 3D objektov. Taktiež si vo väčšom precvičíme prácu s Blenderom a Pythonom a načíme sa nové programátorksé praktiky. V našom prípade nám pôjde o to definovať takú optimalizáciu, ktorá by vyhovovala naším požiadavkám. V prípade optimalizácie 3D modelu pomocou ich modifikácie nám ide o hľadanie tých najoptimálnejších parametrov, ktoré nám umožnia objekt meniť tak aby spĺňal kritériá, ktoré naň kladieme.

Odkazy na materiály

V tejto sekcii nájdete odkazy na materiály, ktoré vám môžu pomôcť pri riešení daných problémov a naučia vás ako používať požívané nástroje:

• Teória - rozcestník stručnej teórie pre koncepty, ktoré potrebujeme
• Rozcestník dokumentácií Blendera - nájdete tu dokumentáciu pre vývojárov, používateľskú ríručku a aj Python API dokumentáciu
• Python syntax - syntax a použitie jazyka Python s ukážkami použitia
• Blender Python API - dokumentácia Python API v Blenderi - nájdete tu všetko čo sa týka programovania s Python API (s knižnicou bpy) v Blenderi
• Platypus - dokumentácia knižnice Platypus s ukážkami použitia

Inštrukcie

1. Zapneme si nástroj Blender a nastavíme si prostredie ako sme sa naučili v predošlých úlohách - necháme si v scéne objekt kocky, prepneme sa do režimu "Scripting" a vytvoríme si tam súbor, do ktorého budeme písať kód.
2. Môžeme si skúsiť pripomenúť prácu s knižnicou bpy z minulých úloh pomocou volania niektorých funkcií. Pre túto úlohu ju budeme potrebovať.
3. Ubezpečíme sa, že máme nainštalovanú knižnicu platypus - skúsime ju importovať pomocou
   

   import platypus
   

   a skúsiť si zavolať nejaký príkaz. Ak nie je nainštalovaná, vieme si ju nainštalovať pomocou príkazu
   

   import site
   import pip
   pip.main(['install', 'Platypus-Opt', '--target', site.USER_SITE])
   

4. Ďalej si vyskúšame prácu s knižnicou. Na tomto odkaze v teórii nájdeme príklad jej použitia: príklad použitia platypus, príklad je stručne aj tu:
   

   from platypus import NSGAII, Problem, Real
   
   def schaffer(x):
       return [x[0]**2, (x[0]-2)**2]
   
   problem = Problem(1, 2)
   problem.types[:] = Real(-10, 10)
   problem.function = schaffer
   
   algorithm = NSGAII(problem)
   algorithm.run(10000)
   

   
   Tento kód si vieme spustiť v Pythone a následne uvidíme výpis výsledkov optimalizácie problému. Ak ho nikde nevidíme, môžeme si otvoriť systémovú konzolu v Blenderi nasledovne:
   
   Toto je definícia problému s 1 premennou 2 cieľmi s funkciou schaffer(x), ktorá priradzuje týmto premenným hodnoty. Keby sme si zobrazili na grafe toto riešenie, vyzeralo by nasledovne: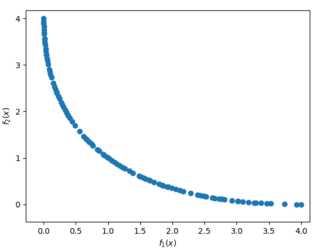
   
   My si budeme chcieť definovať vlastný problém a vlastnú funkciu, ktorá bude slúžiť na ohodnotenie parametrov, ktoré sa budeme snažiť optimalizovať.
6. Optimalizovať budeme parametre meniace náš objekt. Týmito parametrami môže byť napríklad číslo škálovania objektu, alebo úroveň (levels) aplikácie modifikátora "Subdivision Surface." Skúsme si preto vymyslieť modifikácie, ktoré budeme chcieť aplikovať a vytvorme si k ním funkcie podobné funkciám, ktoré inicializujú modifikátori z minulých cvičení.
7. Ďalej si definujeme problém. Potrebujeme si definovať počet parametrov a počet cieľov, ktoré chceme dosiahnuť. Ak by sme chceli napríklad zmenšiť objekt aj zmenšiť počet polygónov a mám pre to vytvorené modifikácie, problém by sme definovali ako Problem(2,2), pretože chceme definovať 2 ciele: zmenšenie objektu a zmenšenie počtu polygónov a chcem to dosiahnuť zmenou 2 parametrov - škálovanie a napríkald úroveň "decimate" modifikátora.
8. Pre optimalizáciu slúži viac algoritmov, my si vyberieme NSGA-II.
9. Tento optimalizačný algoritmus bude spúšťať našu fitness funkciu. Táto funkcia slúži na pridelenie ohodnotenia daným parametrom, ktoré náhodne algoritmus vygeneroval.
10. Je potrebné navrhnť fitness funkciu tak aby správne ohodnocovala a škálovala vracané ohodnotaniea, ktoré zodpovedajú danému modelu a problému, ktorý riešime.

Testovanie a úpravy

Analyzujte či výsledky, ktoré váš optimalizačný algoritmus vracia sú relevantné a vieme ich zužitkovať, návrhy na vylšpeenie máme tu:

• skúste zdokonaliť fitness funkciu tak, že definujte pre každý parameter samotnú ohodnocovaciu funkciu
• skúste si odfiltrovať tie najlepšie a najhoršie ohodnotené riešenia optimalizačného algoritmu a vytvorit si podľa nich modely
• pokúste sa navrhnúť optimalizáciu ďalšieho parametra, to zahŕňa: vytvorenie fitness funkcie, špecifikácia typu a rozsahu parametru (prípadne jeho mapovanie), vytvorenie funkcie, ktorá dané modifikácie na model aplikuje
• vyskúšajte si importovať vlastný objekt a otestovať váš algoritmus na ňom

Spätná väzba

Ak ste spokojní so svojím algoritmom, prezentujte ho ostatným, zhodnoťte koncepty, ktoré ste použili a ako ste ho implementovali, buďte otvorení k hodnoteniam od ostatných a k prípadným návrhom na zlepšenie.

Vzorové riešenie

Ak budete potrebovať motiváciu alebo si skontrolovať váš výsledný model, v nasledujúcich odkazoch nájdete implementáciu daného modelu v nástrojoch, ktoré ste na implementáciu mohli použiť:

• Python

Záver

Týmto cvičením sme si ukázali ako si dokážeme navrhnúť a vytvoriť vlastnú viacúčelovú optimalizáciu a vedieť s ňou vyriešiť vlastný problém, ktorý môže mať aj protichodné kritéria. Vieme na to využiť existujúce knižnice a aplikovať riešenie na výsledné modely.
Pre rozbehanie a prácu Blendera z Visual Studio Code potupujte podľa inštrukcii v tomto videu: Blender + VS Code.